Thanks to firejeep for some diagrams to help me get a clearer picture of what I wanted to rig up to show what happens with loading when you winch. It has taken awhile to get this going due to the visuals not being as clear as I want and some issues with scales for weights. The first were some small digital crane scales. What wasn't clear is there is a hold function that happens when the load quits changing for a few seconds. That became problematic due to an oddity I did not foresee. As I would put a load on the rigging, it would go up 10% above where it would eventually wind up but slowly settle there. The digital scales would lock in a load before the settling finished so it was not clear what you were seeing as far as loads plus hitting the start button and clear button to get them to stay ready to accept load got to be a real pain in the ass. I traded those in for some analog game scales and problem solved.
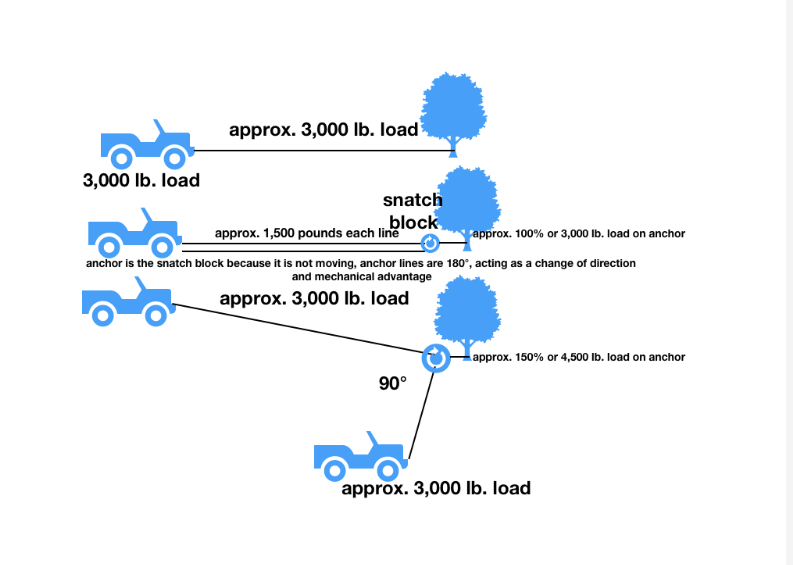
The first scenario we are going to explore is the most common one that leads to confusion and that is a snatch block pull back to the rig to "double" the power of the winch.
Essentially the way it works is each line at the snatch block will have the load of what the winch is putting out. If it is pulling at 5000 lbs, each leg going through the block is 5000 lbs x 2 for a total pulling power of 10,000 lbs.
Here is a diagram from firejeep and then my redneck rigging to illustrate a rig with a winch on it and the anchor points. We will be exploring these three scenarios.
I needed to show the obvious which is the load the rig has against it. The best way to show that was to rig an anchor line with a scale to show it.
Essentially this scale model shows exactly what was predicted and we won't get too nitpicky over frictional issues adding or taking away from the totals.
My version of the second diagram.
1- load moving rig
2- 1st line load
3- 2nd line load
4- anchor load

Load at 1-

Load at 2 and 3

Load at 4

The first scenario we are going to explore is the most common one that leads to confusion and that is a snatch block pull back to the rig to "double" the power of the winch.
Essentially the way it works is each line at the snatch block will have the load of what the winch is putting out. If it is pulling at 5000 lbs, each leg going through the block is 5000 lbs x 2 for a total pulling power of 10,000 lbs.
Here is a diagram from firejeep and then my redneck rigging to illustrate a rig with a winch on it and the anchor points. We will be exploring these three scenarios.
I needed to show the obvious which is the load the rig has against it. The best way to show that was to rig an anchor line with a scale to show it.
Essentially this scale model shows exactly what was predicted and we won't get too nitpicky over frictional issues adding or taking away from the totals.
My version of the second diagram.
1- load moving rig
2- 1st line load
3- 2nd line load
4- anchor load
Load at 1-
Load at 2 and 3
Load at 4

